ミツバチが六角形を使うのには、単純な理由が一つあります。それは、自然界において構築に最も効率的な形だからです。 六角形の格子は、可能な限りの貯蔵スペースと構造的完全性を持つ格子を作成するために、最も少ない量の材料（この場合は蜜蝋）を使用します。これは、数百万年の進化によって洗練された完璧な解決策なのです。
蜂の巣の六角形は偶然の選択ではありません。それは、複雑な工学的問題に対する数学的に最適な解決策です。構築材料の最小化、貯蔵能力の最大化、構造的安定性の確保との完璧な妥協を表しています。
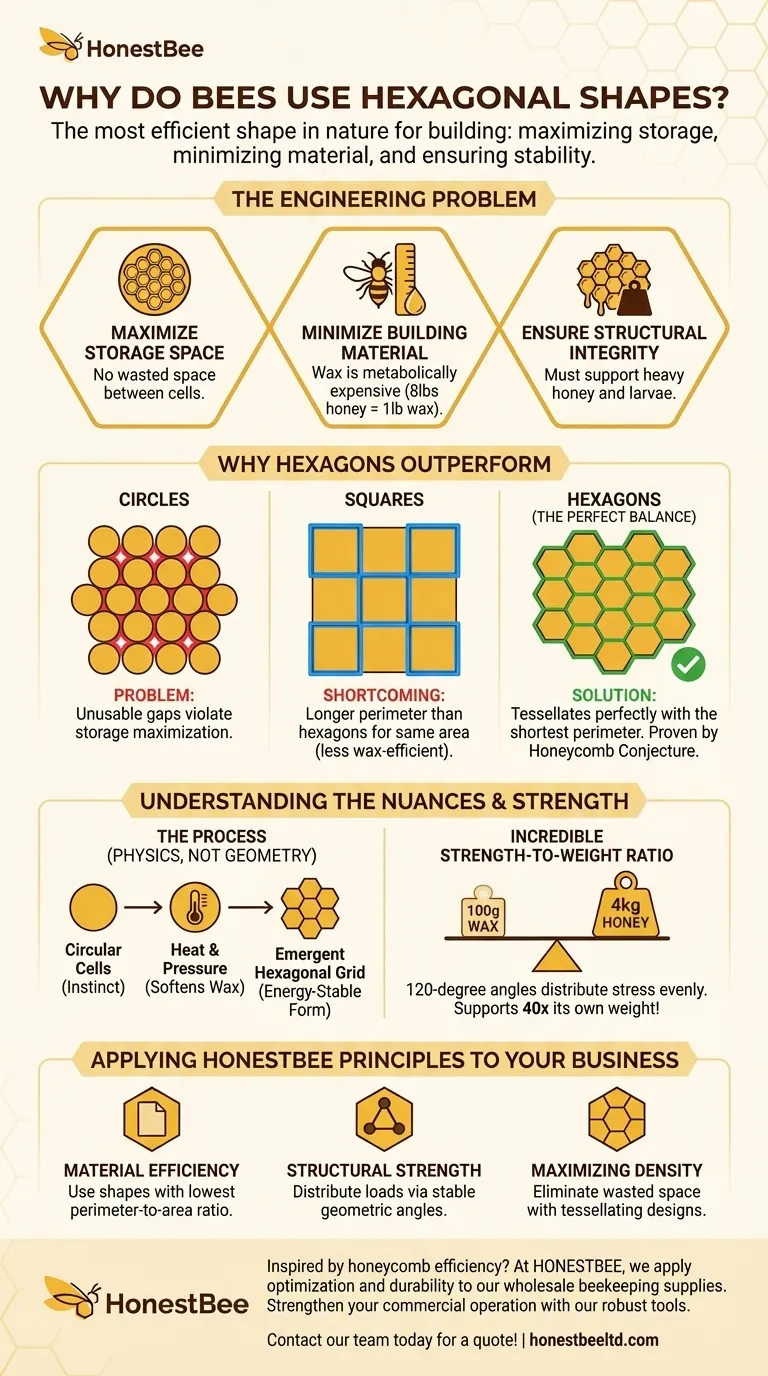
ミツバチが解決しなければならない工学的課題
六角形の天才性を理解するためには、まずミツバチが直面する課題を理解する必要があります。彼らは、次の3つの重要な工学的要件を満たす構造を必要としています。
貯蔵スペースの最大化
コロニーの生存は、可能な限り多くの蜂蜜と花粉を貯蔵できるかどうかにかかっています。したがって、貯蔵セルの形状は、間に無駄な隙間を残さないように、空間効率が高くなければなりません。
構築材料の最小化
ミツバチは、わずか1ポンドの蜜蝋を生成するために約8ポンドの蜂蜜を消費しなければなりません。これにより、蜜蝋は非効率な設計に浪費できない代謝的に高価な資源となります。理想的な形状は、最短の周囲長で与えられた面積を囲む必要があります。
構造的完全性の確保
完成した蜂の巣は信じられないほど重くなります。この構造は、蜂蜜の重さだけでなく、成長途中のミツバチの幼虫の重さも支えるのに十分な強度が必要ですが、それにもかかわらず、比較的壊れやすい素材で作られています。
なぜ六角形は他の形状よりも優れているのか
これらのニーズに対して評価すると、六角形はすべての条件を完全に満たす唯一の形状として浮かび上がります。円や正方形などの他の一般的な形状には、重大な欠点があります。
円の問題点
円は、周囲長が最も短く、最も多くの面積を保持するのに技術的に最も効率的な形状です。しかし、円を詰め込むと、使用できない隙間ができ、貯蔵スペースを最大化するというニーズに反します。
正方形の欠点
正方形、三角形、六角形は、敷き詰め（テッセレーション）できる唯一の正多角形です。つまり、隙間を残さずに平面上にぴったり収まります。正方形は隙間の問題を解決しますが、同じ面積を囲むためには、六角形よりも長い周囲長が必要になるため、蜜蝋の効率が低下します。
六角形の完璧なバランス
六角形が優れているのは、完全に敷き詰められ、かつ敷き詰められる形状の中で最も短い周囲長を持つからです。この原理は非常に根本的であり、「蜂の巣の推測（Honeycomb Conjecture）」として1999年に数学的に証明されました。これは理想的な中間点で、最小の材料コストで最大の貯蔵を提供します。
トレードオフとニュアンスの理解
蜂の巣の完璧な幾何学を賞賛する一方で、そのプロセスは、ミツバチが熟練した建築家であるというよりも、物理学を活用していることによるものです。
意識的な幾何学ではない
ミツバチは角度を意識的に測定しません。この六角形の構造は、本能と物理的な力によって駆動される**創発的特性**です。ミツバチは、互いに接近した、ほぼ円形のセルを構築します。
熱と圧力の力
ミツバチの体温によって発生する熱が蜜蝋を柔らかくします。周囲のセルからの表面張力と圧力が、円形の構造を可能な限りエネルギー的に安定した、最もコンパクトな形状、つまり完璧な六角形の格子へと引き寄せます。
驚異的な強度対重量比
最終的な構造は、効率的な設計の証です。セルの壁が出会う120度の角度は、応力を均等に分散するのに理想的です。これにより、わずか**100グラム**の蜂の巣が最大**4キログラム**の重さを支えることができ、これは自然のエンジニアリングによる驚くべき偉業です。
あなたのプロジェクトへの応用方法
蜂の巣の設計の背後にある原理は、ミツバチに限定されません。それらは、エンジニアリング、設計、ロジスティクスに強力な教訓を提供します。
- 材料効率が主な焦点である場合： 敷き詰めることができ、周囲長と面積の比率が最も低い形状を使用します。六角形が理想的な選択肢です。
- 構造的強度が主な焦点である場合： 蜂の巣が行うように、共有壁と安定した幾何学的角度にわたって荷重を分散させます。
- 密度の最大化が主な焦点である場合： 設計がユニット間に無駄なスペースを排除するように、敷き詰められる形状を使用していることを確認します。
蜂の巣は最適化の極意として立っており、単純な物理的原理がいかにして驚異的に堅牢で効率的な構造を生み出すかを示しています。
要約表：
| 要件 | 六角形が優れている理由 |
|---|---|
| 貯蔵の最大化 | 完全に敷き詰められ、セル間に無駄なスペースを残さない。 |
| 材料（蜜蝋）の最小化 | 敷き詰められる形状の中で、周囲長対面積比が最も短い。 |
| 構造的完全性の確保 | 120度の角度が応力を均等に分散し、驚異的な強度を実現する。 |
蜂の巣の効率に触発されましたか？ HONESTBEEでは、最適化と耐久性の同じ原理を養蜂用品に応用しています。私たちは、商業養蜂場や養蜂機器販売業者に対し、強力で生産的な事業を構築するために必要な、堅牢で高品質なツールを提供します。当社の卸売中心のソリューションがお客様のビジネスをどのように強化できるか、ぜひご相談ください。**見積もりについては今すぐ当社のチームにご連絡ください！**
ビジュアルガイド
関連製品
- 手動蜜蝋コームファンデーションマシン ワックスファンデーションミル エンボスマシン
- 食品グレードのプラスチック製ミツバチフレーム用土台
- 蜜蝋ファンデーションシート 卸売り用ビーハイブファンデーション
- 操作トレイとワックスファンデーションローラー付き電動蜜蝋ファンデーションマシン
- プロフェッショナルなフレーム準備：HONESTBEE 電動ワイヤエンベッダー
